Introduction to Zero Knowledge Proofs
Zero knowledge proofs (ZKPs) are a way for a prover to prove that they have knowledge of a secret without revealing the secret itself. This is done by having the prover convince the verifier that they know the secret by providing a proof that the verifier can verify. The verifier can then be sure that the prover knows the secret without actually knowing the secret themselves. These proofs hold immense potential for enhancing privacy and security in various domains, ranging from financial transactions to identity verification. In this blog post, we will delve into the concept of zero knowledge proofs and explore their application through an example known as the Three Coloring Graph Problem.
Definition of Zero Knowledge Proofs
Zero Knowledge Proofs were first devised in the paper, “The Knowledge Complexity of Interactive Proof Systems” by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in 1985.
The key properties of zero knowledge proofs are:
- Completeness: If the statement is true, an honest prover can convince the verifier of its truth.
- Soundness: If the statement is false, no prover can convince the verifier that it is true, except with some negligible probability.
- Zero knowledge: The verifier learns nothing about the statement other than its truthfulness.
Zero knowledge proofs are based on cryptographic techniques, such as commitment schemes, digital signatures, and hash functions. They employ clever protocols that enable the prover to convince the verifier while maintaining utmost privacy.
Two Abstract Examples
To illustrate the concept of zero knowledge proofs, let’s consider two famous examples:
- The Cave: Imagine there is a circular cave with a door around the curve of the cave. Alice claims to know a secret word that will open the door. Bob is skeptical, so Alice wants to convince him that she knows the secret word without revealing the word itself. How can she do this?
Alice can convince Bob that she knows the secret word by having him stand outside the cave while she goes inside. She then opens the door and walks through it, proving that she knows the secret word. Bob can then verify that Alice knows the secret word without learning the word itself.
- The Color Blind Friend: Suppose Alice is not color-blind and Bob is color-blind. Alice claims to know the color of a ball, but Bob is skeptical. Alice wants to convince Bob that she knows the color of the ball without revealing the color itself. How can she do this?
Two balls are given to Bob, one red and one green. He puts the balls behind his back and randomly chooses to switch them or keep them in the same order. He then brings the balls back out and shows them to Alice. Alice can then tell Bob whether or not he switched the balls. They repeat this process multiple times, and Bob becomes convinced that Alice knows the color of the ball without learning the color itself.
In both of these examples, Alice wants to convince Bob that she knows something without revealing the secret itself. This is the essence of zero knowledge proofs.
The 3-Colorable Graph Problem
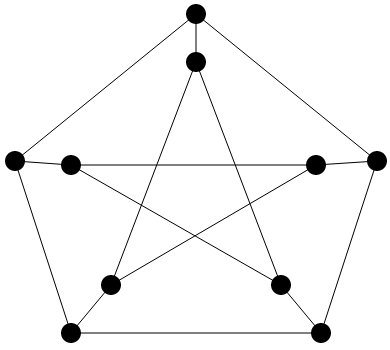
A graph is 3-colorable if the vertices can be colored with three colors such that no two adjacent vertices have the same color. This problem is NP-complete, meaning that it is easy to verify a solution but difficult to find a solution. As a result of it being NP-complete, it means that all NP problems have zero lknowledge proofs.
Here’s how it works:
- The prover will randomly permute the colors of the vertices and use a commitment scheme to commit to the colors
- The verifier will choose any edge and ask the prover to reveal the colors of the vertices
- The prover will reveal the colors of the vertices
- The verifier will verify that the colors are different
- Repeat until the verifier has a high enough confidence that the graph is 3-colorable
There is an excellent website from MIT that has an interactive version of the proof. You can find it here.
Applications of Zero Knowledge Proofs
Zero knowledge proofs have a wide range of applications across various domains, some of which include:
- Cryptocurrencies and Blockchain: Zero knowledge proofs, such as zk-SNARKs and zk-STARKs, are used to verify transactions and smart contracts without revealing the underlying details, ensuring privacy and confidentiality.
- Identity Verification: Zero knowledge proofs can enable individuals to prove their identity or possession of certain credentials without exposing sensitive personal information.
- Password Authentication: Instead of transmitting passwords over a network, zero knowledge proofs can be used to prove knowledge of a password without revealing it, adding an extra layer of security.
Conclusion
Zero knowledge proofs provide a remarkable cryptographic tool for establishing the truth of a statement while preserving privacy. Through the examples we’ve seen how zero knowledge proofs allow a prover to convince a verifier without revealing any additional information. These proofs have significant implications for privacy, security, and trust in various domains, paving the way for innovative applications and the protection of sensitive information.
In our upcoming blog posts, we will explore specific zero knowledge proof protocols, such as zk-SNARKs and zk-STARKs, and dive deeper into their mechanisms and real-world applications. Stay tuned to learn more about the exciting world of zero knowledge proofs!